Parte I: Precisión y Matriz de confusión

Hay muchos tipos de problemas de Machine Learning y, en la mayoría de casos, hay varias maneras en las que nuestro objetivo y los datos que tenemos afectan a cómo medimos el rendimiento de nuestro modelo.

Vamos a empezar con las métricas de evaluación que se usan en modelos de clasificación, hay tres tipos principales de clasificaciones:

• Clasificación binaria: sólo existen dos clases, por lo general una positiva y otra negativa. Por ejemplo, si un paciente sufre una enfermedad o no.
• Clasificación multiclase: en el dataset existen más de una clase, pero las clases son independientes. Por ejemplo un análisis de sentimiento: felicidad, tristeza, preocupación, sorpresa…
• Clasificación multietiqueta: cada muestra puede pertenecer a más de una clase. Por ejemplo al detectar animales en una imagen, podría haber un perro, pero también un perro y un gato en la misma foto.

Dependiendo de las características de nuestro problema, tendremos que elegir una métrica u otra para medir el rendimiento de nuestro modelo.

Por simplicidad, usaremos un problema de clasificación binaria, sin embargo estos métodos pueden generalizarse a otros tipos de problemas.

Precisión en la clasificación

La precisión en la clasificación se define como el cociente entre el número correcto de predicciones y el número total de predicciones:

$$ \text{Precision} = \frac{\text{Predicciones correctas}}{\text{Predicciones totales}} $$

Su métrica complementaria es el error en la clasificación, que se define como el número de predicciones equivocadas dividido entre el número total de predicciones:

$$ \text{Error} = \frac{\text{Predicciones equivocadas}}{\text{Predicciones totales}} $$

Estas métricas son las más simples de interpretar y entender, pero sólo funcionan si tenemos unos datos de entrada balanceados (las clases tienen más o menos el mismo número de elementos) y no tenemos especial interés en predecir ninguna de las clases.

Matriz de confusión

La matriz de confusión representa la suma de valores predichos y los valores reales. Ayuda a entender cuántas de las muestras han sido clasificadas de manera correcta e incorrecta en cada una de las clases.

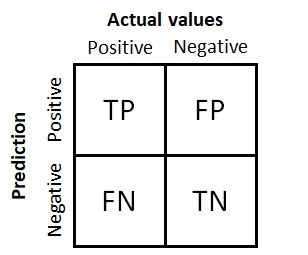
Matriz de confusión para un problema de clasificación binaria

La matriz tiene cuatro cuadrantes:

• Positivos verdaderos (PV, TP en inglés): Número de muestras positivas que han sido clasificadas como positivas.
• Negativos verdaderos (NV, TN en inglés): Número de muestras negativas que han sido clasificadas como negativas.
• Falsos positivos (FP): Número de muestras positivas que han sido clasificadas incorrectamente como negativas, a este error se le conoce como Error de tipo I, que se refiere al rechazo incorrecto de la hipótesis nula.
• Falsos negativos (FN): Número de muestras negativas que han sido clasificadas incorrectamente como positivas. Este error se conoce como Error de tipo II, que se refiere al error de no rechazar la hipótesis nula.

En general, el objetivo de cualquier modelo es el de maximizar el número de PV y NV y, por lo tanto, minimizar el de FP y FN.

Para sacar el número total de muestras o predicciones, se deben sumar los valores de los cuatro cuadrantes:

$$ \text{Predicciones totales} = PV + NV + FN + FP $$

La matriz de confusión nos permite computar métricas más complejas y redefinir otras más simples:

$$ \text{Precision} = \frac{PV + NV}{PV + NV + FN + FP} $$

$$ \text{Error} = \frac{FP + FN}{PV + NV + FN + FP} $$

El resto de métricas de evaluación se explicarán en el siguiente artículo.