Parte II: Precision/Recall y Sensitivity/Specificity
El el artículo anterior de métricas de evaluación para clasificación explicamos que la accuracy es una métrica muy útil y muy fácil de interpretar. Sin embargo, si los datos de entrada no están balanceados, no sirve para nada.
También definimos qué es la matriz de confusión, en la que se definen cuatro categorías sobre nuestras predicciones: Positivos Verdaderos (True Positives en inglés, TP), Negativos Verdaderos (True Negatives en inglés, TN), Falsos Positivos (False Positives en inglés, FP) y Falsos Negativos (False Negatives en inglés, FN). Esta información es útil para evaluar nuestro modelo incluso si nuestros datos de entrada no están balanceados.
Precision-Recall
Por un lado, precision (precisión) indica la proporción de muestras relevantes o positivas predichas por nuestro modelo que son positivas de verdad:
$$ \text{Precision} = \frac{TP}{TP + FP} $$
Por otro lado, el recall (recuerdo) indica la proporción de muestras relevantes o positivas predichas por nuestro modelo respecto a todas las muestras que son positivas:
$$ \text{Recall} = \frac{TP}{TP + FN} $$
La siguiente figura ilustra ambas métricas:
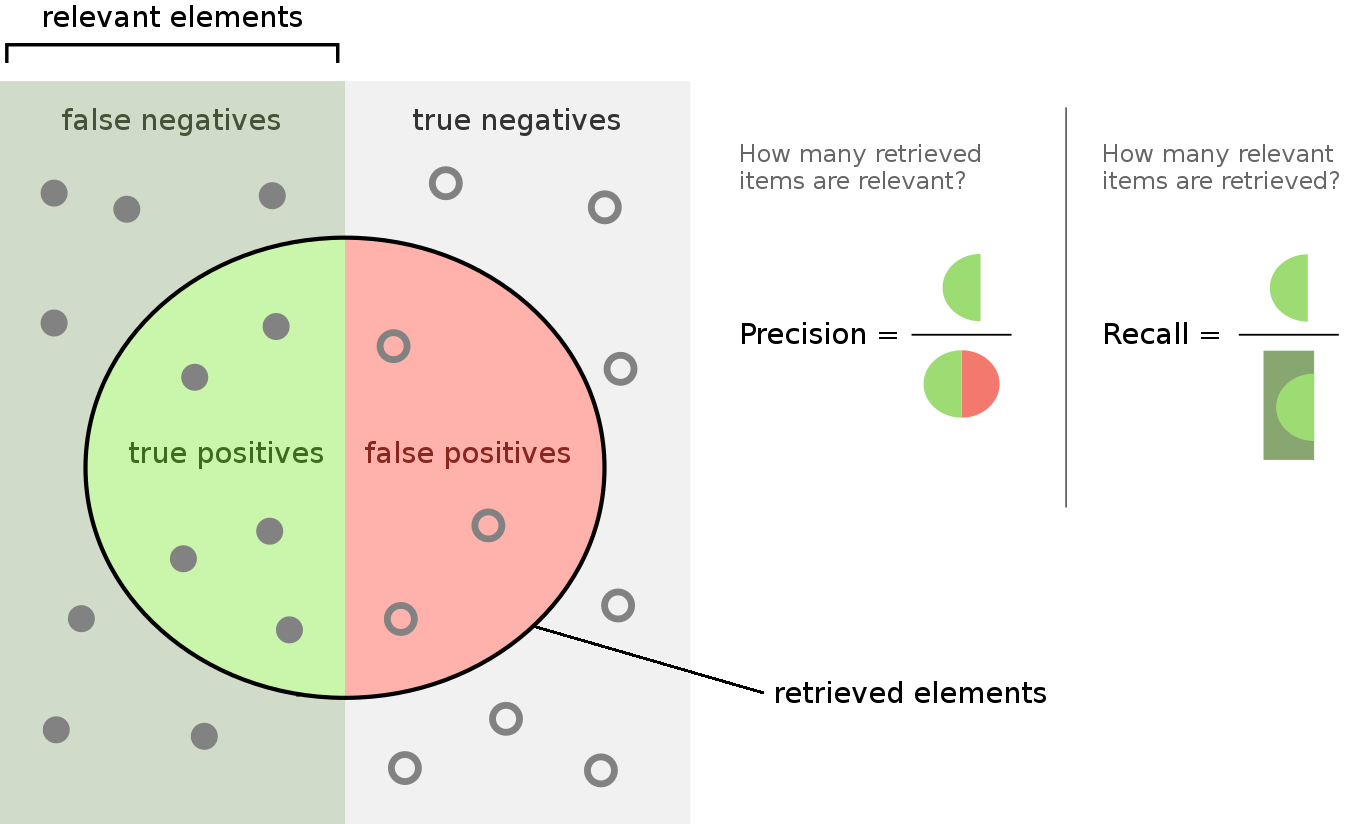
Como hemos comentado, estas métricas son robustas a datasets no balanceados. Una manera de usar ambas métricas como evaluación es usar el Fbeta-score (puntuación Fbeta):
$$ F_{ \beta}\text{ -}score = \frac{(1 + \beta^2) \times Precision \times Recall}{\beta^2 \times Precision + Recall} $$
El Fbeta-score se define como la media armónica de la precision y el recall. El parámetro beta puede ser ajustado dependiendo de la situación:
- Si el objetivo del análisis es reducir el número de FP, entonces se elige una beta pequeña para incrementar la importancia de la precision en la matriz
- Si el objetivo es reducir el número de FN, entonces se elige una beta grande para incrementar la relevancia del recall en la métrica
- Para alcanzar un equilibrio entre FP y FN, se usa el valor de beta = 1, en este caso esta métrica se conoce como F1-score (puntuación F1) ya que es muy común, y la ecuación anterior se transforma en:
$$ F_1\text{-}score = 2 \times \frac{Precision \times Recall}{Precision + Recall} $$
Sensitivity-Specificity
Otra manera de evaluar un modelo es con las métricas de sensitivity (sensibilidad) y specificity (especifidad). Estas métricas también son robustas a datasets no balanceados.
Sensitivity indica lo bien que se ha predicho la clase positiva y es equivalente al recall:
$$ \text{Sensitivity} = \frac{TP}{TP + FN} $$
Specificity es la métrica complementaria e indica lo bien que se ha clasificado la clase negativa:
$$ \text{Specificity} = \frac{TN}{FP + TN} $$
Similar a lo que pasa con la precision y el recall, ambas métricas pueden combinarse con la geometric mean (media geométrica) o G-Mean:
$$ \text{G-Mean} = \sqrt{Sensitivity \times Specificity} $$



0 Comments