Gradiente descendente

Gradiente Descendente o Descenso del Gradiente (en inglés Gradient Descent) es un algoritmo de optimización para encontrar el mínimo local de una función. Busca la combinación de parámetros que minimiza la función de coste.

Para que el Gradiente Descendente funcione, la función de coste debe ser diferenciable y convexa.

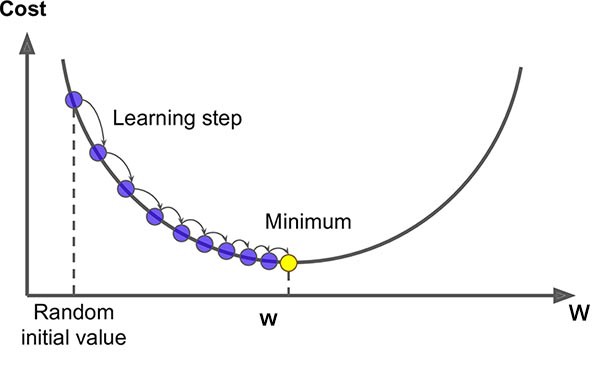
Visualización del Gradiente descendente, función de coste (Cost) y pesos (W).
Fuente: openaccess.uoc.ed

Pasos

1. Se define una función de hipótesis y se inicializan sus pesos (o coeficientes): se asignan valores aleatorios de bajo valor a los pesos (θ₀, θ₁…).

$$ h_\theta(x) = \theta_0 + \theta_1 x $$

Ejemplo de función de hipótesis

2. La variable dependiente de la función de hipótesis se calcula usando esos coeficientes para cada dato de entrada.

3. La función de coste (la suma de los residuos al cuadrado) se calcula:

$$ J = \frac{1}{2m} \sum_{i=1}^{m} (h(x^{(i)}) – y^{(i)})^2$$

Función de coste, versión rigurosa aquí

4. Calculamos los gradientes: las derivadas parciales del coste se calculan para encontrar la dirección que minimiza la función de coste.

$$\frac{\partial}{\partial \theta_j} J(\theta_0, \theta_1)$$

Cálculo de gradientes

5. Nos movemos en la dirección opuesta a los gradientes: el parámetro de ratio (α), que es un factor de escala que controla cuánto cambian los coeficientes de una iteración a otra, se aplica a los gradientes y se sustrae a los coeficientes, que se actualizan.

$$ \theta_j := \theta_j – \alpha \frac{\partial}{\partial \theta_j} J(\theta_0, \theta_1)$$

Actualización de los coeficientes

6. El proceso se repite desde el paso 2 hasta que se llega a un error mínimo y ya no hay mejoras posibles.

Tipos de Gradiente Descendente

Hay tres maneras de calcular un Gradiente Descendente:

Gradiente Descendente Batch

• Usa todos los datos de entrada para calcular los gradientes en cada iteración y actualizar los coeficientes
• La solución óptima se alcanza de manera suave
• Esta operación es muy costosa computacionalmente, ya que todo el dataset ha de estar cargado en memoria para hacer cálculos sobre él

Gradiente Descendente Estocástico

• Elige un dato al azar de los datos de entrada en cada iteración para calcular los gradientes en ese punto y actualizar los coeficientes
• La solución óptima se alcanza después de varias iteraciones ya que los datos pueden ser muy distintos en cada paso
• El coste computacional es más bajo que con el Batch, ya que sólo una instancia de los datos se calcula en cada iteración, por contra se necesitan más iteraciones

Gradiente Descendente Mini-batch

• Esta solución usa una mezcla entre las dos anteriores, coge una pequeña muestra de los datos de entrada al azar en cada iteración para calcular el gradiente y actualizar los pesos
• El proceso de optimización tiene menos ruido que en el método estocástico ya que se usan más instancias para actualizar los coeficientes, pero no llega a ser tan suave como el Batch
• El coste computacional es el mínimo de todos los métodos, ya que sólo cargamos una pequeña parte de los datos y requiere un menor número de iteraciones

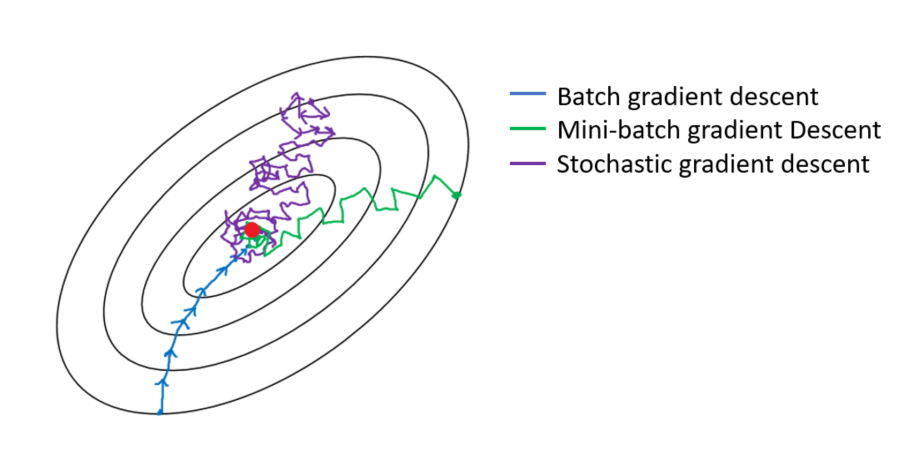
Ilustración de cómo los distintos métodos llegan al óptimo

El Gradiente Descendente Batch es el que menos tarda en encontrar la solución, pero requiere muchos recursos. El Gradiente Descendiente Estocástico es ligero computacionalmente, pero requiere muchas iteraciones para encontrar el óptimo. El Gradiente Descendiente Mini-Batch usa lo mejor de los dos mundos.