Implementación básica de K-Means

Setup

En un artículo anterior, explicamos el algoritmo de K-Means. Para llegar a entenderlo mejor, lo vamos a implementar en Python desde cero. Para instalar todas las herramientas necesarias puedes seguir nuestros artículos de setup para Windows o para Linux.

Para mejorar la presentación de este artículo, sólo vamos a enseñar las partes esenciales del código, para descargarte el código completo descárgalo de nuestro repositorio.

Lo primero que necesitamos hacer es abrir un notebook de Jupyter (o mejor aún, el notebook de nuestro repositorio). Para hacer eso abre una terminal y activa tu entorno virtual. Te recomendamos que vayas a la carpeta que contiene el código que te acabas de descargar y que ejecutes:

jupyter notebook

Esto ejecutará Jupyter y nos dará una URL en el propio terminal. Copia y pega esa URL en el navegador que quieras (la URL suele tener la siguiente pinta: http://localhost:8888/?token=26e0ed28a7df8511c8789376d422dd36bc015a1403efd7cb).

Si todo ha ido bien, deberías de ver algo como esto:

Haz click en el archivo “Basic K-Means.ipynb” y juega con el código.

Los datos

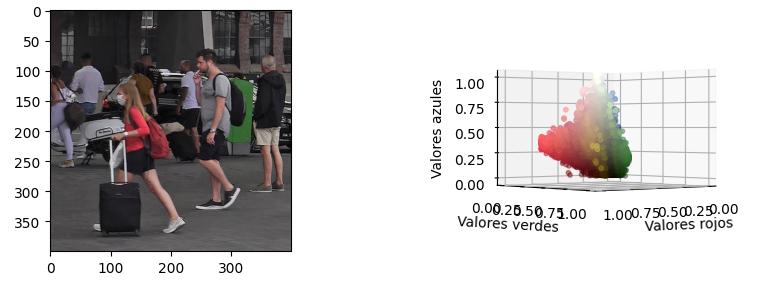
Hemos preparado una imagen de test de licencia CC0 (la podemos usar libremente). Si vas a usar cualquier otra imagen te recomendamos que sea pequeña, ya que K-Means tardará mucho más según el tamaño de la imagen. Como ves en la imagen anterior, las visualizaciones del notebook muestran la imagen al lado de su gráfico scatter 3D. Este scatter muestra los píxeles de la imagen como puntos tridimensionales, usando los canales RGB como coordenadas XYZ. Además, cada punto tiene el color de su pixel original. Esto nos permite tener una nube de puntos para ver cómo el algoritmo de K-Means agrupa los píxeles juntos.

Algoritmo de K-Means

def k_means(centroides, data_points, iteraciones_maximas=10):
    
    # Estructuras donde guardamos a qué clúster pertenece cada punto
    clusters = [[] for x in range(len(centroides))]
    indices = [[] for x in range(len(centroides))]
    
    centroides_anteriores = None

    # Bucle principal
    for i in range(iteraciones_maximas):
        
        # Le asignamos a cada punto el clúste más cercano
        for indice_del_punto, punto in enumerate(data_points):
            
            dist = float('inf')
            # Índice del centroide candidato
            centroide_candidato = 0
            
            for indice_del_centroide, centroide in enumerate(centroides):
                
                # Calculamos la distancia entre el punto y el centroide
                d = np.linalg.norm(punto-centroide)
                
                # Si estamos más cerca de este centroide, le 
                # asignamos a este punto ese centroide
                if d < dist:
                    dist = d
                    centroide_candidato = indice_del_centroide
            
            # Ahora sabemos que indice_del_punto pertenece a centroide_candidato
            clusters[centroide_candidato].append(punto)
            indices[centroide_candidato].append(indice_del_punto)
            
        # Ahora recalculamos los centroides haciendo la media por centroide
        centroides = ([np.mean(np.array(clusters[x]), axis=0) 
                      for x in range(len(centroides))])
        
        # Si los centroides no han cambiado, hemos llegado al límite
        # Hemos de usar ese generador porque tenemos un array de arrays de numpy
        if (centroides_anteriores != None 
            and not all([np.array_equal(x, y) 
                         for x, y in zip(centroides_anteriores, centroides)])):
            print("Saliendo del bucle")
            break
            
        # Actualizamos los centroides anteriores
        centroides_anteriores = centroides
        
    return (centroides, indices)

La implementación de nuestro algoritmo de K-Means recibe 3 parámetros de entrada y devuelve 2 listas:

Parámetros de entrada

• centroids: Los centroides iniciales de nuestro datase. Simplemente elegimos K puntos al azar del dataset.
• dataset: Una lista con todos los puntos del dataset
• max_iterations: Este es un parámetro opcional para limitar el número máximo de iteraciones del algoritmo K-Means. K-Means para su ejecución si alcanza el número máximo de iteraciones o si los centroides no se han movido

Parámetros de salida

• centroids: Una lista de K elementos con los valores de los centroides
• indexes: Una lista que nos indica a qué cluster pertenece cada punto de nuestro dataset inicial. Por ejemplo, si indexes = [0, 0, 1], los dos primeros puntos de nuestro dataset pertenecerán al cluster 0, y el tercer punto pertenecerá al cluster 1

Visualizando valores distintos de K

Visualizar los resultados de los algoritmos de Machine Learning puede ser muy complicado. Para este artículo hemos creado una visualización que puede que te ayude a comprender cómo se han formado los clusters en mayor detalle. Hemos usado el scatter de RGB que hemos explicado arriba, pero ahora hemos pintado cada punto con el valor de su centroide. El centroide de cada clúster es la media de todos sus puntos, así que cada cluster es del color medio de sus puntos. Usando el slider de abajo, vas a poder cambiar entre distintos valores de K. Te animamos a que explores los gráficos e identifiques los distintos clusters. Algunas preguntas interesantes que te puedes plantear:

• ¿Cuándo consigue el color verde su propio clúster? ¿Por qué tan tarde?
• ¿Por qué el rojo está tan presente?
• De K=10 a K=20 los cambios visuales no son muy grandes, ¿Por qué?

En caso que quieras pensar sobre esas preguntas, hemos ocultado las respuestas, si sientes que ya sabes la respuesta pasa el ratón por encima de los bloques negros.

• ¿Cuándo consigue el color verde su propio clúster? ¿Por qué tan tarde?: Hay muy poco verde en la imagen y sus puntos están muy cerca de clusters grandes
• ¿Por qué el rojo está tan presente?: Si expliras los gráficos, verás que los valores de rojo están muy separados del resto, esto significa que el rojo de la imagen es muy vivo y “captura” otros clústers
• De K=10 a K=20 los cambios visuales no son muy grandes, ¿Por qué?: La mayoría de clústes se crean cerca de los colores oscuros ya que hay una gran densidad de puntos en esa zona, visualmente los colores oscuros no resaltan tanto