Regularización

Al entrenar un modelo de Machine Learning, pueden pasar varias cosas:

• El modelo puede overfit (sobreentrenarse), lo cual significa que está aprendiéndose demasiado los datos de entrada, es demasiado complejo y se ha aprendido patrones muy específicos o aleatorios (como puede ser el ruido). Esto es un problema porque el modelo no tendra un buen rendimiento con datos reales.
• El modelo puede underfit (no estar lo suficientemente entrenado) lo cual significa que es muy simple y no lo suficientemente flexible. Por lo tango no ha llegado a aprenderse los patrones importantes de los datos de entrada.
• El modelo no es ni demasiado complejo ni demasiado simple, puede encontrar los patrones relevantes en los datos de entrada pero sin aprendérselos. Este es el escenario ideal, el que queremos para nuestro modelo.

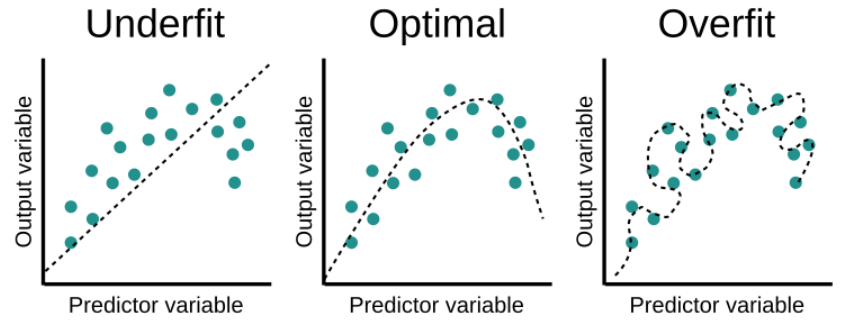
Posibles estados del entrenamiento, fuente: educative.io

Hay varias técnicas para identificar en qué estado nos encontramos y cómo alcanzar el modelo ideal. Una de esas maneras es usando la regularización.

Primero, consideremos la fórmula de Regresión Lineal Múltiple:

Let’s first consider the Multiple Linear Regression formula:

$$ y^{(i)} = B_0 + B_1 x_1^{(i)} + … + B_n x_n^{(i)} $$

Hay que tener en cuenta que cada uno de los coeficientes (B) determina la contribución de un atributo de nuestros datos. Por lo tanto, nuestros datos tienen n atributos diferentes. El índice i representa un dato en concreto.

En regresión lineal, la función de optimización es la de suma de cuadrados de los residuos:

$$\mathrm{J} = \sum_{n=1}^{n} (y^{(i)}-\hat y^{(i)})^2 = $$

$$ = \sum_{i=1}^{n} (y^{(i)}- B_0 – B_1 x_1^{(i)} – … – B_n x_n^{(i)})^2 $$

El modelo se ha entrenado estimando los coeficientes B de tal manera que minimicen esa función. Si los datos de entrada contienen ruido, los coeficientes no generalizarán de manera correcta y el modelo no podrá predecir correctamente.

Regularización

La regularización reduce el efecto del ruido en nuestro modelo. Reduce el peso de los coeficientes que están asociados al ruido, lo que reduce su contribución a la predicción. Para la regresión lineal, esto se consigue limitando los coeficientes para que tengan valores estimados cercanos al cero, que resulta en un modelo más simple y menos flexible que previene el overfitting.

Hay varios métodos de regularización, aquí cubrimos las dos principales que se aplican a regresión lineal:

Regresión Ridge

En estadísticas se conoce como la Norma Vectorial L-2 (L-2 norm). Esta técnica consiste en añadir una pequeña cantidad de bias a nuestro modelo, con el objetivo de mejorar las predicciones. Esto lo hacemos añadiendo un término de penalty o shrinkage (penalización o empequeñeción), que es el hiperparámetro λ multiplicado por la suma de los cuadrados de cada atributo individual.

Por lo tanto, la función de optimización se transforma en:

$$\mathrm{J}_{Ridge} = \mathrm{J} + \lambda (B_1^2 + … + B_n^2) $$

λ controla cuánta regularización queremos aplicar a nuestro modelo. Lo elegimos mediante un proceso llamado tuneado de hiperparámetros. Si λ vale cero, la función de optimización se convierte en la de regresión lineal.

Por un lado, las regresiones Ridge ayudan cuando hay una gran colinearidad entre atributos. Además ayuda cuando hay más atributos que muestras.

Por otro lado, esta técnica de regularización minimiza el valor de los coeficientes pero nunca llegan a cero, por lo que no se puede usar para selección de atributos. Además no ayuda a la interpretabilidad del modelo, ya que no reduce el número de variables independientes, sólo su contribución.

En Python se puede usar en la librería de scikit-learn sklearn.linear_model.Ridge.

Regresión Lasso

Esta regularización se conoce como la Norma Vectorial L-1 (L-1 Norm). Parecido a lo que hemos hablado de la regresión Ridge, la regresión Lasso introduce un término de penalty (penalización) que consiste en el hiperparámetro λ multiplicado por la sima del peso absoluto de cada atributo individual.

Por lo tanto, la función de optimización se transforma en:

$$\mathrm{J}_{Lasso} = \mathrm{J} + \lambda (|B_1| + … + |B_n|) $$

La regresíon Lasso sí que puede forzar sus coeficientes a valer cero, por lo tanto esta regularización es útil para hacer selección de atributos.

Este método tiene limitaciones, por ejemplo si tienes menos muestras que atributos, la regresión Lasso sólo considerará tantos coeficientes como número de muestras, lo cual implica que pueda ignorar algunos coeficientes importantes. Además tiene problemas de interpretabilidad, por ejemplo si hay atributos que estén muy correlados, la regresión Lasso seleccionará uno al azar.

Como con la regresión Ridge, la regresión Lasso se puede usar en Python con la librería de scikit-learn sklearn.linear_model.Lasso.

Esta ha sido una pequeña introducción a las dos técnicas principales de regresión lineal. En próximos artículos indagaremos en las matemáticas y en por qué Lasso quita completamente la contribución de algunos atributos mientras que Ridge sólo los reduce.