Modelos ARIMA-GARCH

Los modelos ARCH/GARCH pueden asistir o mejorar el pronóstico de los modelos ARIMA .

En primer lugar, los datos de las series temporales deben ser estacionarios para que estos modelos sean aplicables. Si no, deberíamos aplicar algunas transformaciones como la diferenciación. Dado que estos modelos se utilizan principalmente en finanzas, en adelante nos referiremos a los rendimientos del precio (price returns), que son el resultado de aplicar el diferencial a los precios de las acciones.

Los rendimientos ( rₜ ) se pueden modelar como:

$$ r_t=\mu_t + \varepsilon_t $$

Se puede descomponer en dos componentes:

• Media ( μₜ ): esto se puede representar mediante un modelo ARIMA.
• Término de error ( εₜ ): se refiere a los residuos después de ajustar un modelo del valor medie como ARIMA. Para ciertas aplicaciones como finanzas, la varianza puede cambiar constantemente con el tiempo, con períodos de alta o baja volatilidad, también llamados agrupamiento de volatilidad. Los modelos ARIMA no son capaces de capturar estos cambios de varianza o volatilidad a lo largo del tiempo, lo que llamamos heteroscedasticidad . Esto puede tener un gran impacto en ciertas aplicaciones, por ejemplo, en la evaluación del riesgo de las inversiones. Si este cambio en la varianza está autocorrelacionado con el tiempo, se pueden usar modelos ARCH/GARCH para capturarlo.

Modelos ARCH/GARCH

Los modelos ARCH/GARCH esperan que los datos sean estacionarios y sin otros componentes como tendencia o estacionalidad, solo cambios en la varianza. Recordemos las diferencias entre ellos:

• ARCH modela el cambio en la varianza a lo largo del tiempo como una función de los errores residuales de un proceso de valor medio.
• Los modelos GARCH son una extensión de los modelos ARCH que incorporan un componente de media móvil junto con el componente autorregresivo. Además de los errores residuales de los períodos anteriores (lags), también incluye los términos de varianza de los lags anteriores de un proceso de media.

Estos modelos tienen dos aplicaciones principales:

1. Volatilidad del pronóstico
2. Considerar la varianza de los residuos del modelo ARIMA para mejorar el pronóstico

Pronóstico de volatilidad

Podemos suponer una media constante o cero para los rendimientos y ajustar directamente un modelo ARCH/GARCH.

Estos son los pasos a seguir:

1. Obtener los rendimientos (cambio porcentual) de los datos
2. Estimar los parámetros “q” para los modelos ARCH, o “q” y “p” para los modelos GARCH mirando el PACF de los rendimientos al cuadrado
3. Probar modelos de orden superior para encontrar el que minimiza el AIC
4. ¡Pronosticar la volatilidad!

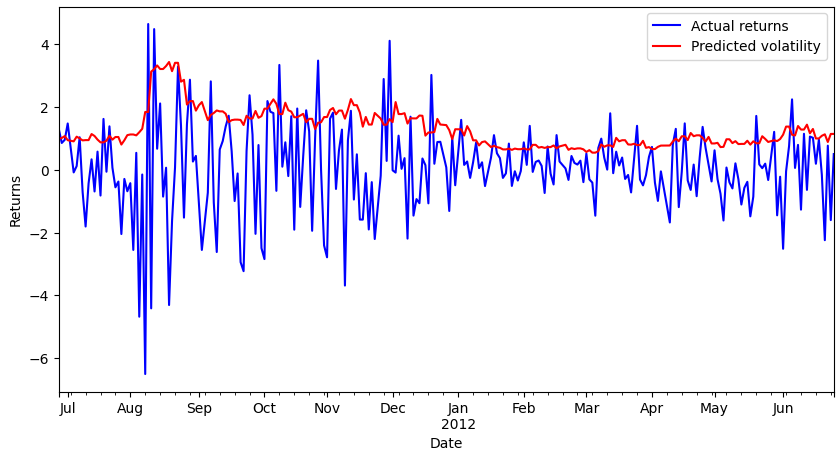
A continuación puede ver las predicciones de volatilidad tras ajustar un modelo ARCH(11) sobre los rendimientos del precio del S&P500.

Modelo ARIMA-GARCH

Un modelo ARIMA-GARCH tendrá en cuenta el cambio de varianza para mejorar la previsión de precios o rendimientos.

Los pasos a seguir son:

1. Obtener los rendimientos (cambio porcentual) de los datos
2. Ajustar un modelo ARIMA:
   1. Encontrar los parámetros óptimos “p” y “q”
   2. Ajustar modelo a los datos de entrenamiento
   3. Comparar con los rendimientos reales para obtener los residuos del modelo
3. Comprobar la heteroscedasticidad en los residuos. Por ejemplo, comprobando el PACF de los residuos al cuadrado. Además, podríamos usar el test de Ljung-Box o el test del multiplicador de Lagrange.
4. Ajustar un modelo ARIMA-GARCH. Aquí tenemos dos opciones:
   1. Ajustar un modelo GARCH sobre los residuos del modelo ARIMA y sume ambas contribuciones.
   2. Ajustar ambos modelos simultáneamente. Esta es la forma preferida ya que, de lo contrario, las estimaciones de ARIMA pueden ser inconsistentes.
5. ¡Pronósticar los rendimientos! También puede agregar intervalos de confianza precisos gracias al modelo de varianza.

Artículos de series temporales

1. Introducción a los modelos ARIMA
2. Selección de parámetros en modelos ARIMA
3. ARIMA estacional
4. Modelos ARCH/GARCH para Series Temporales
5. Modelos ARIMA-GARCH