Introduction to ARIMA models

A time series is a series of data points ordered in time. Time is often the independent variable and the objective is usually to make a forecast for the future.

It has many applications, some of which are forecasting sales, stock prices, temperatures or even the number of COVID cases!

Traditionally, time series have relied on statistical methods such as ARIMA, Holt or ETS. However, in recent years Machine Learning and Deep Learning methods have gained importance in this field.

ARIMA

ARIMA is one of the most popular traditional statistical methods. It stands for Auto-Regressive Integrated Moving Average.

It is composed of 3 components:

1. AR: Auto-Regressive
2. I: Integrated
3. MA: Moving Average

For now, we will assume that our time series doesn’t have a seasonal component.

Auto-Regressive (AR)

AR models use a linear combination of past values of the variable of interest.

They are described by the parameter “p “, which refers to the number of previous values to consider for the forecast.

The equation corresponding to this model is:

$$y_t = c + \phi_1 y_{t-1} + \phi_2 y_{t-2} + …+ \phi_p y_{t-p} + \varepsilon_t$$

• c : represents a constant or drift
• y : refers to the current value of the variable of interest (t), value one timestep before (t-1), value two timesteps before (t-2)…
• ϕ : are the coefficients that need to be calculated by fitting the training data
• p : is the number of coefficients that we want our model to have
• εₜ : is the error term, which is white noise

Moving Average (MA)

MA models use a linear combination of past error values instead of previous values of the variable of interest.

They are characterized by the parameter “q “, which refers to the number of previous error values to consider for the forecast.

The equation corresponding to this model is:

$y_t = c + \theta_1 \varepsilon_{t-1} + \theta_2 \varepsilon_{t-2} + … + \theta_q \varepsilon_{t-q} + \varepsilon_t$

• c : represents a constant or drift
• y : refers to the variable of interest
• θ : are the coefficients that need to be calculated by fitting the training data
• q : is the number of coefficients that we want our model to have
• εₜ : is the error term, which is white noise

Integrated (I)

It refers to the differentiation of the time series data. This doesn’t represent a model by itself. It is just a way of extending the applicability of the AR, MA or ARMA models. ARMA models (without the I) are valid only for stationary time series.

What does stationary mean?

In layman’s terms, a time series is stationary if its mean and variance do not vary across time.

There are several ways of achieving this:

• Time series differencing
• Power transformation
• Log transformation

Time series differencing

Differencing refers to calculating the difference between the current time period and the previous time period. In some fields like finance, it is often seen the percentual change instead, which simply consists of applying a 100 factor to the previous transformation.

How to achieve stationarity with an ARIMA model?

We can just apply differencing to yₜ, which is on the left-hand side of the equation and leave the right-hand side unaltered. We should apply the differencing as many times as necessary to achieve a stationary time series. This will be specified through the parameter “d “.

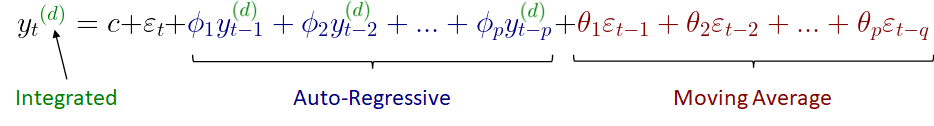
We will then have the three ARIMA components plus a constant c and the error term εₜ which will be just white noise.

The constant will be calculated during the model training, however, the error will be just the difference between our forecast and the actual value, and we will only be able to calculate it once we know the actual value of our variable of interest yₜ, and this case will not correspond to a forecast anymore…

What p, q and d parameters should we use?

Check the next article in the series to discover how to select the three parameters.

Time Series articles

1. Introduction to ARIMA models
2. Parameters selection in ARIMA models
3. Seasonal ARIMA
4. ARCH / GARCH models for Time Series
5. ARIMA-GARCH models