Parte II: Eliminar la estacionalidad y normalizar los datos

En la primera parte de esta serie, vimos que la limpieza de datos es un paso esencial en el proceso de análisis de series temporales. Este consta de los siguientes subpasos:

1. Tratar valores faltantes
2. Quitar tendencia
3. Quitar estacionalidad
4. Comprobar la estacionariedad y hacerlo estacionario si fuera necesario
5. Normalizar los datos
6. Eliminar valores atípicos
7. Suavizar los datos

Este artículo servirá de guía general para eliminar la estacionalidad y normalizar los datos de series temporales. Recuerda que dependiendo de tus datos, deberás saltarte algunos pasos o modificar o añadir otros.

Quitar estacionalidad

Antes de comenzar, podríamos usar la biblioteca statsmodels de Python para ver la descomposición estacional de los datos antes de eliminar la tendencia. Este no es un paso obligatorio, pero podría ser útil para visualizar los componentes de los datos de la serie temporal. Antes de usarlo, debemos seleccionar el período de estacionalidad. Dado que estamos trabajando con producción mensual de cerveza, podemos suponer que los datos tendrán algún tipo de estacionalidad durante el año y que esto debería repetirse a lo largo de los años. Por lo tanto, estableceremos el período en 12 (12 meses ya que tenemos una frecuencia mensual en nuestros datos y asumimos una estacionalidad anual).

# Importar librería
import statsmodels.api as sm

# Descomponer datos seleccionando la frecuencia adecuada
decomp = sm.tsa.seasonal_decompose(
  df['Produccion mensual de cerveza'], period=12)
decomp_plot = decomp.plot()

# Mostrar resultado
plt.xlabel('Fecha')
decomp_plot.set_figheight(10)
decomp_plot.set_figwidth(10)
plt.show()

Como era de esperar, podemos ver un pico de producción cada año y una tendencia suave sin altibajos, solo la tendencia real a lo largo de los años. También podemos ver los residuales, que hacen referencia a todo el ruido o anomalías durante este periodo de tiempo después de extraer el componente estacional y la tendencia.

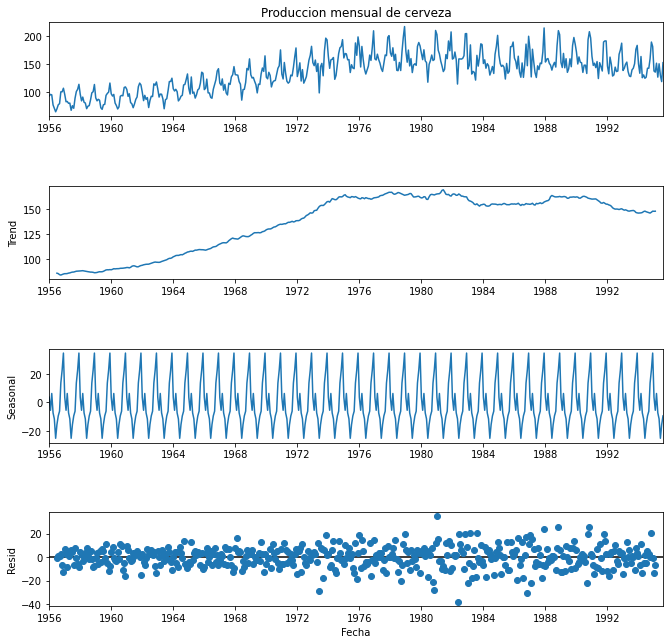
Debemos prestar atención a la magnitud de los diferentes componentes. Por un lado, la tendencia debe ser grande en comparación con el componente estacional, pero el componente estacional debe ser relevante y lo suficientemente grande como para poder decir que hay estacionalidad. Por otro lado, la mayoría de los valores de los residuos deben ser pequeños y estar distribuidos aleatoriamente, sin embargo, pueden aparecer algunos valores grandes en aquellos casos en los que haya un valor atípico claro. Podemos decir que este es el comportamiento que observamos en nuestros datos.

Una forma de deshacerse de la estacionalidad y suavizar los datos podría ser teniendo en cuenta solo el componente de tendencia. ¡Solo tendremos que recordar agregar este componente después de hacer el pronóstico!

Otra posibilidad podría ser no hacer nada con la estacionalidad y dejarla en los datos. En este caso, necesitaríamos utilizar un modelo capaz de tratar con estacionalidad como SARIMA .

Sin embargo, si vamos a utilizar un enfoque de Machine Learning, posiblemente eliminarlo ahora sea el paso más lógico. Usaremos un enfoque más intuitivo para esto.

# Calcula la media anual
media_anual = df_cerveza.groupby(df_cerveza.index.month).mean()
mapped_media_anual = df_cerveza.index.map(
    lambda x: media_anual.loc[x.month])

# Estandarizar la media mensual
df_cerveza = df_cerveza / mapped_media_anual

# Plot outcome
df_cerveza.plot(figsize=(15,5))
plt.xlabel('Fecha')
plt.ylabel('Ratio de producción de cerveza estandarizada')
plt.grid()
plt.show()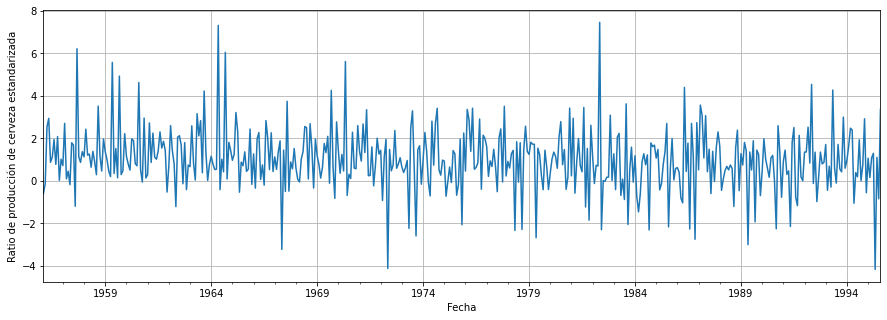

Podemos ver ahora que el resultado parece bastante aleatorio y, por lo tanto, estacionario. Podríamos comprobar si este es realmente el caso.

Comprobar la estacionariedad

La estacionariedad se refiere a una propiedad de los datos donde las propiedades estadísticas como la media, la varianza y la estructura de autocorrelación permanecen constantes a lo largo del tiempo. En otras palabras, una serie temporal estacionaria tiene media constante, varianza constante y su autocovarianza es independiente del tiempo.

Esta propiedad es importante porque nos permite modelar el proceso subyacente que genera los datos y hacer predicciones basadas en ese modelo. La no estacionariedad, por otro lado, puede dificultar el modelado y el pronóstico de los datos, ya que las propiedades estadísticas de la serie temporal pueden cambiar con el tiempo.

Hay algunas pruebas o tests estadísticos que se pueden usar para verificar la estacionariedad en una serie de tiempo. Pero primero, debemos introducir el concepto de raíz unitaria. Una raíz unitaria se refiere a un parámetro cuyo valor es igual a uno en el modelo autorregresivo (AR). Los dos tests principales para verificar la estacionariedad son:

• Test de Dickey-Fuller aumentada (ADF): se utiliza para verificar la presencia de una raíz unitaria en los datos de la serie temporal, que es una causa común de no estacionariedad. La hipótesis nula ($H_0$) es que los datos no son estacionarios, y el rechazo de esta hipótesis indica que los datos son estacionarios.
• Test de Kwiatkowski-Phillips-Schmidt-Shin (KPSS): este test se utiliza para verificar la presencia de tendencia en los datos, que también puede causar no estacionariedad. La hipótesis nula ($H_0$) es que los datos son estacionarios, y el rechazo de esta hipótesis indica la presencia de una tendencia.

Ten en cuenta que las hipótesis nulas para estas dos pruebas son contrarias, por lo tanto, deberemos tener cuidado al interpretar los p-values.

Realicemos ambos tests usando las funciones en la biblioteca statsmodels :

# Importa las librerías requeridas
from statsmodels.tsa.stattools import adfuller, kpss

# Efectuar un test ADF
resultado = adfuller(df_cerveza)
print('Test ADF:\tp-value: {:.3f}'.format(resultado[1]))

# Efectuar un test KPSS
resultado = kpss(df_cerveza)
print('Test KPSS:\tp-value: {:.3f}'.format(resultado[1]))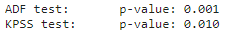

Para el test KPSS, debemos verificar si el p-value es mayor que el nivel de significación. En este caso es inferior a 0.05, por lo que no es estacionario según este test.

Todavía tenemos que trabajar para hacer que nuestros datos sean estacionarios. Simplemente podemos aplicar otra diferenciación y realizar ambos tests de nuevo.

# Diferenciar nuestros datos una vez más
df_cerveza = df_cerveza.diff()[1:]

# Efectuar un test ADF
resultado = adfuller(df_cerveza)
print('Test ADF:\tp-value: {:.3f}'.format(resultado[1]))

# Efectuar un test KPSS
resultado = kpss(df_cerveza)
print('Test KPSS:\tp-value: {:.3f}'.format(resultado[1]))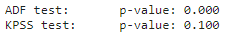

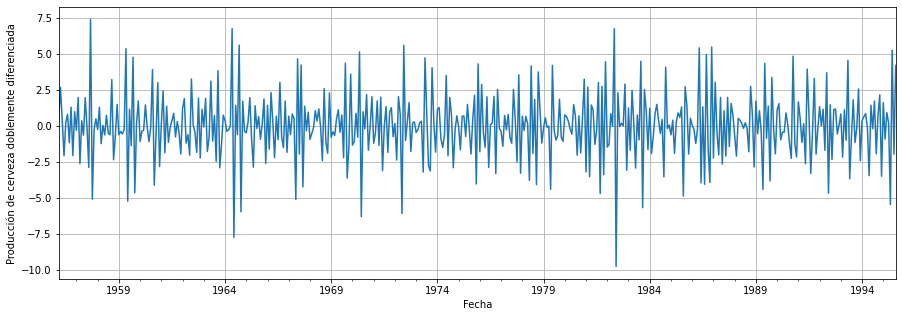
Normalizar los datos

El siguiente paso es llevar los datos a una misma escala, a esto se llama normalización. Hay diferentes técnicas:

1. MinMax Scaler: este método o escalador escala cada valor a un rango determinado, generalmente entre 0 y 1. Es útil cuando se desea conservar la distribución original pero se quiere ajustar la escala de los datos.
2. Standard Scaler: este método escala los datos para que tengan una media cero y una varianza unitaria. Es equivalente a calcular la z-score de los datos. Es útil cuando la distribución de los datos no es normal y se desea normalizarlos a una distribución gaussiana estándar.
3. Robust Scaler: este método es resistente a valores atípicos en los datos y escala los datos al IQR (rango intercuartílico). Es útil cuando tiene datos con valores extremos que podrían sesgar el proceso de escalado.
4. MaxAbs Scaler: este método escala cada valor al valor absoluto máximo de esa característica. Es útil cuando los datos están centrados alrededor de cero y se desea conservar la dirección y el signo de cada entidad.

Usaremos el Standard Scaler, ya que será útil más adelante para eliminar los valores atípicos. Hay dos alternativas aquí: el enfoque intuitivo y usar la biblioteca scikit-learn.

El enfoque intuitivo es muy fácil y sencillo de implementar:

# Calcular la media y la desviación típica
media = df_cerveza.mean()
desviacion = df_cerveza.std()

# Normalizar datos
df_cerveza = (df_cerveza - media) / desviacion

Podemos lograr el mismo resultado con la función de scikit-learn:

# Importar librería
from sklearn.preprocessing import StandardScaler

# Crear un objeto StandardScaler
escalador = StandardScaler()

# Convertir datos a numpy array y cambiar tamaño
array_cerveza = df_cerveza.values.reshape(-1, 1)

# Ajustar escalador a los datos y transformarlos
datos_escalados = escalador.fit_transform(array_cerveza)

# Reconvertir a pandas Series
df_cerveza = pd.Series(datos_escalados.flatten(), 
                    index=df_cerveza.index, name='Mes')

Ambos resultados serán iguales. Dos consideraciones antes de terminar:

• Si opta por el enfoque scikit-learn, podrá probar fácilmente otras técnicas simplemente reemplazando StandardScaler por MinMaxScaler, MaxAbsScaler o RobustScaler.
• Asegúrese de guardar los valores de media y la desviación estándar en el primer enfoque y el objeto escalador en el segundo para poder volver a los valores de producción de cerveza después de realizar el pronóstico con el modelo.

Podemos terminar mostrando cómo se ven los datos normalizados:

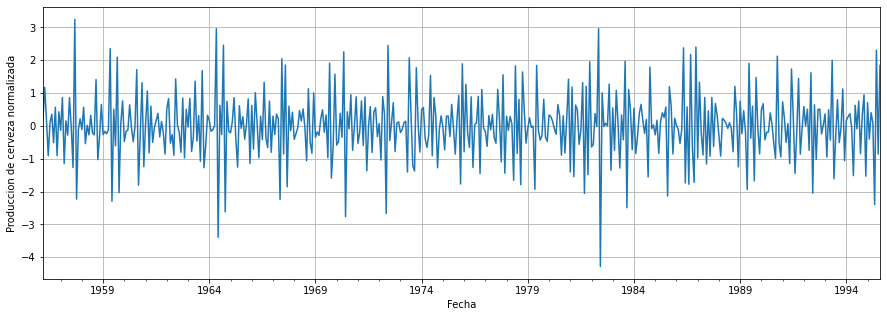
Finalmente podemos decir que nuestros datos son estacionarios y normalizados. ¡Ahora estamos un paso más cerca de poder comenzar a construir nuestro modelo!

Puedes acceder al Jupyter notebook en nuestro repositorio:

GitHub – MLPills-Es/quitar-estacionalidad-y-normalizar-datos: Un Jupyter notebook que cubre los básicos de quitar estacionalidad, forzar estacionareidad y normalizar los datos.

Un Jupyter notebook que cubre los básicos de quitar estacionalidad, forzar estacionareidad y normalizar los datos. – GitHub – MLPills-Es/quitar-estacionalidad-y-normalizar-datos: Un Jupyter notebook que cubre los básicos de quitar estacionalidad, forzar estacionareidad y normalizar los datos.

github.com

Para ejecutarlo ahora mismo, haga clic en el icono de abajo:

¡Veremos en el próximo artículo cómo podemos verificar y eliminar la estacionalidad!