Content-based recommender systems

Content-based recommender systems have emerged as a pivotal tool in the digital age, where the vastness of online content can often be overwhelming. These systems utilize various algorithms to analyze and filter information, providing personalized recommendations to users based on their individual preferences and behavior. By doing so, they help to enhance the user experience, making it easier for people to find content that is relevant and appealing to them.

One of the main strengths of content-based recommender systems is their ability to harness the power of data to deliver accurate and targeted recommendations. By analyzing user profiles and content metadata, these systems can identify patterns and correlations that might not be immediately apparent. This allows them to make informed predictions about what content a user is likely to enjoy, thereby increasing the likelihood that the user will engage with the recommended content. In this article, we will delve into the mechanics of content-based recommender systems, exploring how they work and how you can build your own.

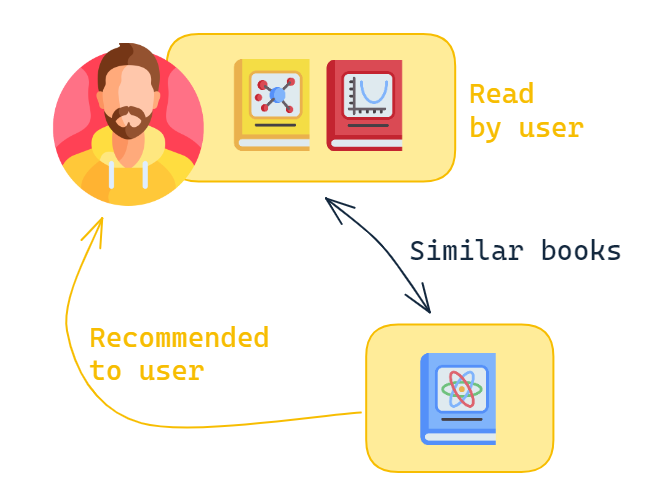
Here is an example with books. We have data about the books a particular user has read. We can then find similar books to those in our database of books and recommend to this user the top matches.

Data

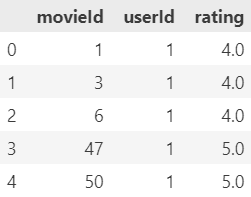
First, we need to import the data. We will use the MovieLens dataset, a dataset that is widely used for recommendation system research. It was created by the GroupLens research group at the University of Minnesota. It contains user ratings for movies, as well as movie metadata such as genres and release dates. The ratings are given on a scale of 1 to 5, with 5 being the highest rating.

We will use two files:

• ratings: it includes the ratings that each user has given to each of the movies they have watched.
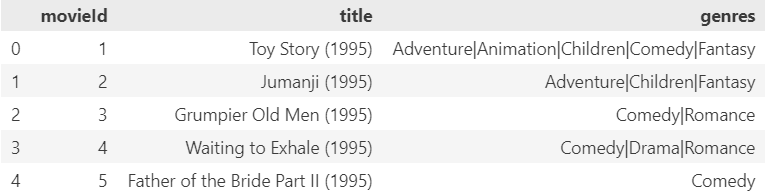
• movies: it includes the movie ID, the title (with the release year) and the genres of each movie.

import pandas as pd

# Ratings
ratings = pd.read_csv('ml-latest-small/ratings.csv')
ratings_df = ratings[['movieId', 'userId', 'rating']]
ratings_df.head()

# Movies
movies = pd.read_csv('ml-latest-small/movies.csv')
movies.head()

Now that we have the data loaded we need to find out how similar each movie is to the rest. For that, we can use the information we have about movie genres and the release years.

Genres similarity

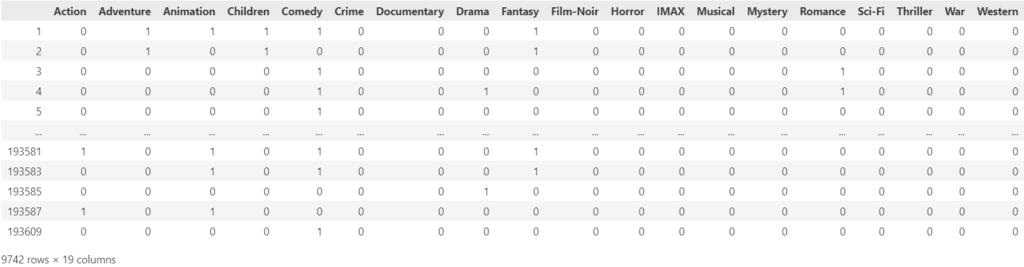
Let’s get the genres in different columns, since we have them all packed in the genres column.

genre_df = movies['genres'].str.get_dummies(sep='|')
genre_df = genre_df.drop(columns=[genre_df.columns[0]])
genre_df.index = movies.movieId.values

Once we have it ready we can compute the similarity between them. We will use cosine similarity, which is a method used to calculate the similarity between two vectors by finding the cosine of the angle between them. The cosine similarity between two vectors $\mathbf{A}$ and $\mathbf{B}$ is calculated as follows:

$$\text{Cosine Similarity} = \cos(\theta) = \frac{\mathbf{A} \cdot \mathbf{B}}{\|\mathbf{A}\| \cdot \|\mathbf{B}\|}$$

Where,

• $ \mathbf{A} \cdot \mathbf{B} $ is the dot product of the two vectors.
• $ |\mathbf{A}| $ and $|\mathbf{B}| $ are the magnitudes (or Euclidean norms) of the vectors $ \mathbf{A} $ and $ \mathbf{B} $, respectively.

From there, we will obtain a similarity matrix. This is a square matrix used to show the similarity between different items. Each cell in the matrix represents the similarity between two items, with the row and column indices corresponding to the items being compared. The value in the cell represents the degree of similarity between the items, with higher values indicating greater similarity.

We will convert it (it is a numpy array) into a dataframe and we will set as index and header the movie IDs.

from sklearn.metrics.pairwise import cosine_similarity
import numpy as np

# Compute the similarity matrix
similarity_matrix = cosine_similarity(genre_df)

# Convert to DataFrame and add movies IDs to index and header
similarity_df = pd.DataFrame(similarity_matrix, columns=movies.movieId.values, index=movies.movieId.values)

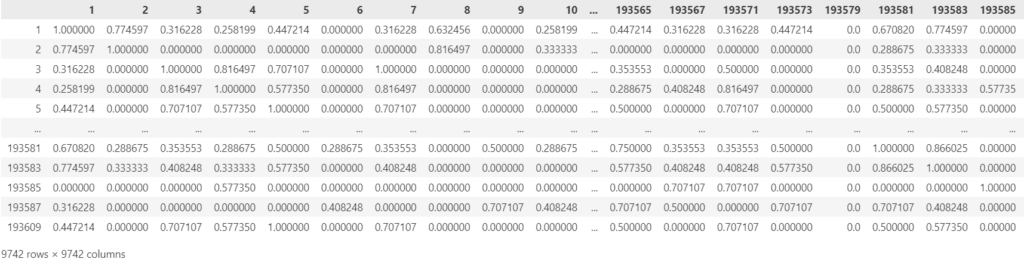
This matrix represents the similarity of each movie with the others between 0 and 1. For example, the movie with ID 1 and the movie with ID 2 have a similarity of 0.7746. The higher the better, so in this case they are quite similar in terms of genre. However, the movie with ID 1 and the one with ID 4 are way less similar. Note that the diagonal is all full of ones, that is because each movie is the most similar to itself.

Release year similarity

Before computing this similarity we need to extract the years each movie were released. We notice that the year is in the title.

movies_year = movies.copy()
movies_year[['Title', 'Year']] = movies_year['title'].str.extract(r'(?P<Title>.*?)\s*\((?P<Year>\d{4})\)')#.isna().sum()
movies_year = movies_year.dropna()
movies_year['Year'] = movies_year['Year'].astype(int)
movies_year = movies_year.drop(columns=['genres'])

Now we need to define a function that computes how similar movies are according to their release year. We used the exponential function of their difference divided by 10:

$$ \text{sim} = \exp\left(-\frac{\left|\text{Year}_{\text{movie1}} – \text{Year}_{\text{movie2}}\right|}{10}\right) $$

import math

def compute_year_similarity(df, movie1, movie2):

    diff = abs(movies_year.loc[movie1, 'Year'] - movies_year.loc[movie2, 'Year'])
    sim = math.exp(-diff / 10.0)
    return sim

Time to compute the similarity. We create a matrix full of zeros that we are going to fill in with the similarity value. This will take some time. To speed up things here we are taking advantage of this matrix being symmetric, so we compute only half of it.

# Initialize a matrix with zeros of shape (# movies, # movies)
similarity_matrix_year = np.zeros((len(movies_year.index), len(movies_year.index)))

# Iterate over each movie index and movie name
for i, movie1 in enumerate(movies_year.index):
    for j, movie2 in enumerate(movies_year.index):
        
        # Check if the movie indices are different and if the similarity value has not been computed yet
        if i < j and similarity_matrix_year[i][j] == 0.0:
            
            # Compute the year similarity between movie1 and movie2
            similarity_matrix_year[i][j] = compute_year_similarity(movies_year, movie1, movie2)
            
            # Since the similarity matrix is symmetric, set the value at (j, i) to be the same as (i, j)
            similarity_matrix_year[j][i] = similarity_matrix_year[i][j]
        
        # If the movie indices are the same, set the similarity value to 1
        elif i == j:
            similarity_matrix_year[i][j] = 1
 
# Convert it into a dataframe and assign movie IDs to the index and header           
similarity_year_df = pd.DataFrame(similarity_matrix_year, columns=movies_year.movieId.values, index=movies_year.movieId.values)

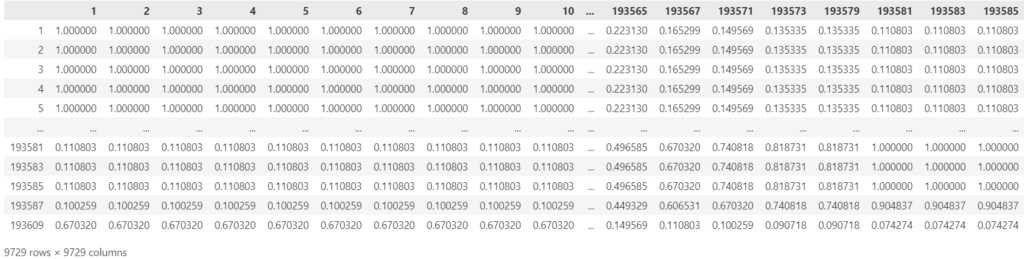
Get the global similarity matrix

There are multiple approaches you can use here:

• Weighted Average:
  $$\text{global_similarity} = w_1 \times \text{genre_similarity} + w_2 \times \text{release_year_similarity}$$
• Multiplication: $$\text{global_similarity} = \text{genre_similarity} \odot \text{release_year_similarity}$$
• Minimum: $$\text{global_similarity} = \min(\text{genre_similarity}, \text{release_year_similarity})$$
• Minimum: $$\text{global_similarity} = \max(\text{genre_similarity}, \text{release_year_similarity})$$
• Harmonic Mean: $$\text{global_similarity} = \frac{2 \times \text{genre_similarity} \times \text{release_year_similarity}}{\text{genre_similarity} + \text{release_year_similarity}}$$
• Geometric Mean: $$\text{global_similarity} = \sqrt{\text{genre_similarity} \odot \text{release_year_similarity}}$$

In the above formulas, $w_1$ and $w_2$ are the weights for the genre and release year similarity matrices, respectively, and they add up to 1. Also ⊙ represents the element-wise multiplication of the matrices.

For simplicity, we will just multiply both similarity matrices, so if either the genres or the year are not appealing to the user, the global similarity will be low.

# Get global similarity matrix
global_similarity_df = similarity_df * similarity_year_df

# Fix those cases in the release year similarity matrix in which the title didn't contain a valid year
global_similarity_df.fillna(0.0, inplace=True)

Offer top n recommendations

The next step is to create a function able to recommend similar movies to the ones the user has previously watched and rated.

These are the steps followed:

1. Item Representation:
   • This refers to creating a profile for each item, which represents the important characteristics of the item, in our case these were the genres and the release year.
2. User Profile:
   • Once the items are represented, the next step is to build a user profile that represents the user’s preferences.
   • This can be done by analyzing the user’s past behavior, such as the items they have interacted with, liked, or rated highly.
   • The user profile is typically a weighted sum of the item profiles that the user has interacted with. The weights could be determined by the user’s ratings or by some other measure of the user’s preference for each item.
3. Matching:
   • After building the user profile, the next step is to find items that are similar to the user’s preferences.
   • This involves comparing the user profile to each item profile in the dataset to find items that are similar or closely match the user’s preferences.
   • This comparison can be done using similarity measures such as cosine similarity, Euclidean distance, or any other suitable metric. In our case, we used the cosine similarity.
4. Recommendation:
   • Finally, the system recommends the items that are most similar to the user’s preferences.
   • This could involve ranking the items based on their similarity to the user profile and recommending the top-N items.
   • The recommendations could also be filtered or adjusted based on additional constraints or criteria, such as the user’s location, age, or other demographic information.

# Create dictionary to map movie IDs to movie titles
movieId_to_title = movies.set_index('movieId').loc[:,['title']].to_dict()['title']

def get_top_n_recommendations(user_id, similarity_matrix=global_similarity_df, n=10, movieId_to_title=movieId_to_title):

    # Filter the ratings for the target user
    user_ratings = ratings_df[ratings_df['userId'] == user_id]

    # Merge the user's ratings with the similarity matrix
    merged = user_ratings.merge(similarity_matrix, left_on='movieId', right_index=True)

    # Calculate the weighted average of the similarity scores for each movie
    weighted_averages = merged.iloc[:, 3:].multiply(merged['rating'], axis=0).mean(axis=0)

    # Sort the weighted averages
    sorted_weighted_averages = weighted_averages.sort_values(ascending=False)
    sorted_weighted_averages = sorted_weighted_averages.to_frame(name='rating')
    sorted_weighted_averages['title'] = sorted_weighted_averages.index.map(movieId_to_title)
    sorted_weighted_averages = sorted_weighted_averages.reset_index(names=['movieId'])

    # Get the top-N recommendations
    top_n_rec = sorted_weighted_averages.head(n)
    top_n_rec.index = top_n_rec.index + 1
    print(f'Top recommended movies for user {user_id}: {top_n_rec.title.values}')

    return top_n_rec

Let’s try with one user:

# Select a user ID
user_id = 55

# Check this user's ratings
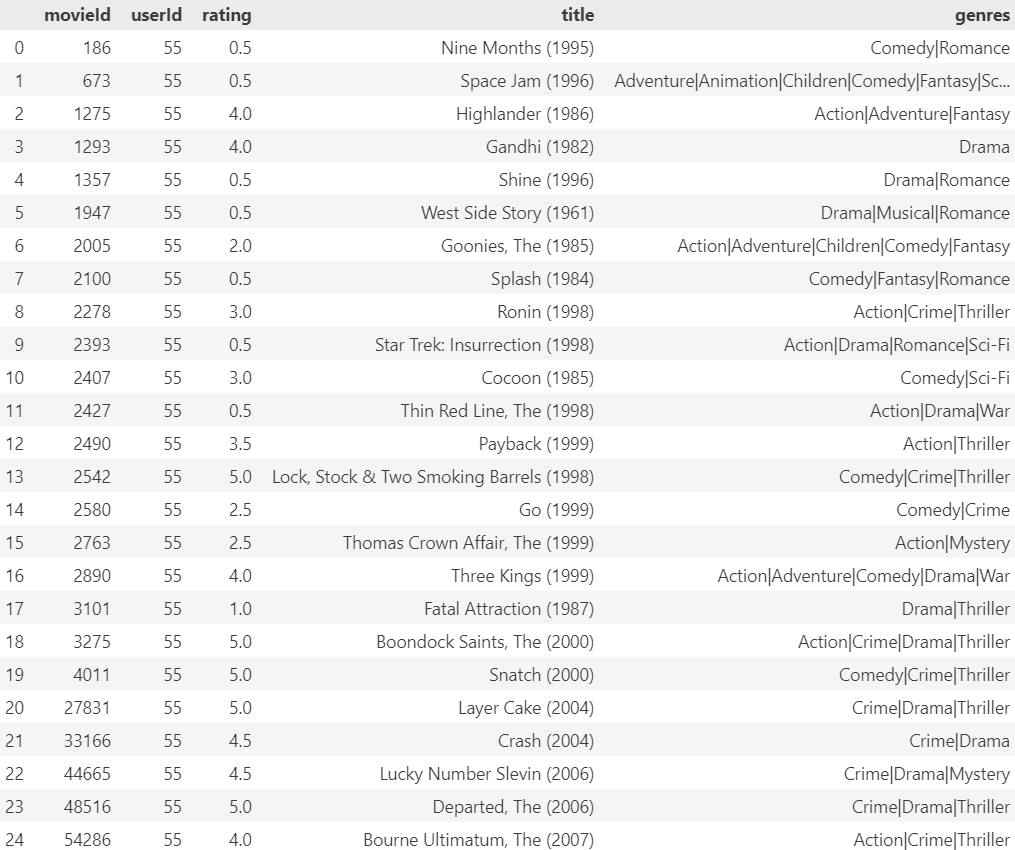
ratings_df[ratings_df.userId == user_id].merge(movies, left_on='movieId', right_on='movieId')

Let’s get the top 10 recommendations based on those ratings:

get_top_n_recommendations(user_id)

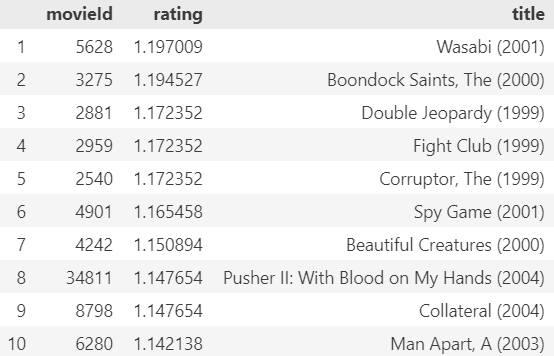
We could check if the genres match the preferences of this user. But doing a quick check, we can see that the release years match the preference of the user.