Los modelos ARIMA son simples pero muy potentes a la hora de hacer series temporales. Los introdujimos en un artículo anterior, sin embargo los parámetros se han de elegir correctamente para que produzcan una predicción precisa.
Un modelo ARIMA(p,d,q) se define por tres parámetros:
- p: Orden autoregresivo (autoregressive order)
- d: Orden de diferencia (difference order)
- q: Orden de media móvil (moving average order)
¿Qué valores de p, q y d debemos utilizar?
¿Cómo podemos estimar d?
Como se explica en el artículo anterior, necesitamos un modelo estacionario.
El test estadístico que se emplea para verificar la estacionaridad de una serie temporal es el test Augmented Dickey-Fuller.
Las hipótesis de este test son:
- H₀ (Hipótesis nula) = La serie temporal no es estacionaria
- H₁ (Hipótesis alternativa) = La serie temporal es estacionaria
Debemos definir un nivel de significancia a, que generalmete tiene un valor de 0.05. Esto se usa para compararlo con el valor p (p-value) del test. Por un lado, si el p valor del test es mayor que el nivel de significancia, fallaríamos en rechazar la hipótesis nula, lo que significa que serie temporal no seríá estacionaria. Por otro lado, si el p valor es menor que le nivel de significancia, rechazaremos la hipótesis nula, lo que significa que nuestra serie temporal se puede considerar estacionaria.
Para elegir d haremos ese test en los datos de la serie temporal. Si podemos concluir que es estacionaria entonce d valdrá 0. Si no lo es, necesitaremos aplicar una transformación de diferenciación y volver a realizar el test. Si tras una diferenciación nuestra serie temporal se vuelve estacionaria, d valdrá 1. Este proceso se repetirá tantas veces como sea necesarias hasta definir d.
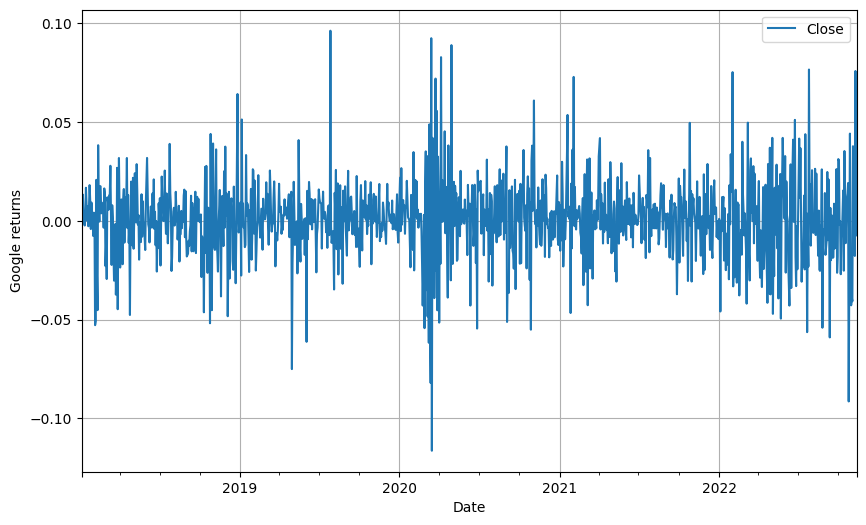
Ejemplo de una serie temporal estacionaria, el precio de las acciones de Google
¿Cómo estimamos p y q?
Necesitamos comprobar cómo de correlada esta la serie temporal con versiones lagged (retrasadas) de sí misma.
A la serie temporal original se refiere como 0. Una versión retrasada 1 paso temporal se refiere como 1, y así todas. La correlación con la serie temporal original con retraso de 0 (sin retraso), siempre valdrá 1 ya que son la misma serie temporal.
Necesitamos diferenciar dos correlaciones:
- La correlación indirecta que los pasos temporales t-1, t-2, t-3… tienen sobre el paso temporal t simplemente por ser adyacentes los unos a los otros. Por ejemplo, con valores de acciones, el precio de hoy vendrá influenciado por el precio que tuvo ayer y, por lo tanto, el precio de ayer tiene relación con el precio que tuvo anteayer.
- La correlación directa que cada uno de los pasos temporales anteriores tiene con el paso temporal t. Continuando con el mismo ejemplo, imagina que cada tres días hay un evento especial, es de esperar que veremos una correlación directa con la serie temporal retrasada 3 pasos.
Para medir estos efectos podemos usar los gráficos ACF y PACF:
- ACF Función de autocorrelación (AutoCorrelation Function) muestra la correlación entre pasos temporales. Incluye los efectos directos e indirectos
- PACF Función parcial de autocorrelación (Partial AutoCorrelation Function) muestra sólo la correlación directa
Se usan los gráficos de “piruleta” (lollipop) para visualizarlos:
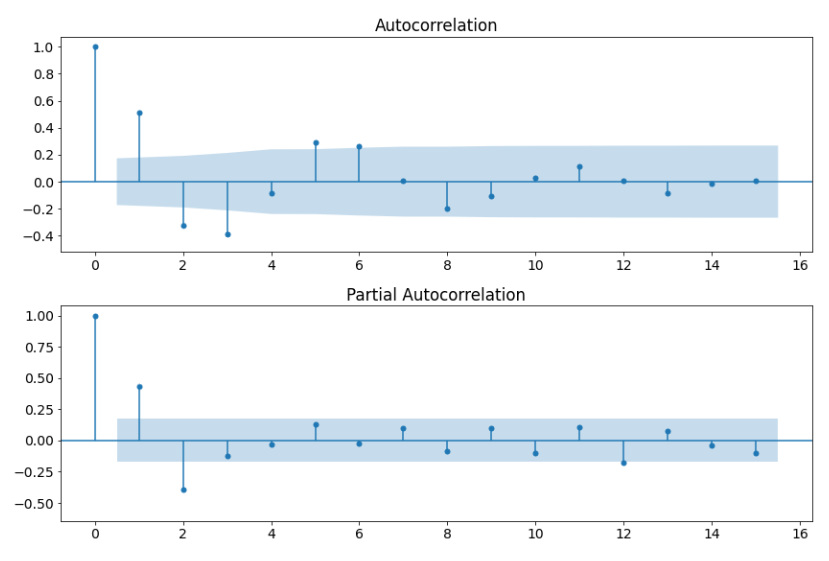
Ejemplo de gráficos ACF y PACF
Hay varias líneas o “piruletas” en ellos. Las piruletas indican la correlación en cada retraso (en el eje X) respecto a la serie temporal original. Necesitamos prestar atención a las piruletas más altas cerca del retraso 0 que están fuera de la zona azul. Si una piruleta está en este área, esto significa que la correlación no es significativamente respecto al 0 y, por lo tanto, no es relevante.
- Para el parámetro p que determina cuántos valores anteriores tendremos en cuenta para la parte AR de ARIMA, necesitamos comprobar el gráfico PACF ya que estamos interesados en la correlación directa
- Para el parámetro q que determina cuántos residuos (errores) anteriores necesitamos tener en cuenta para la media móvil, necesitamos mirar el gráfico ACF ya que buscamos principalmente la correlación indirecta
Crea tu propio modelo
Si quieres crear tu propio modelo, puedes estudiar los siguientes notebooks que he creado en Kaggle:
- Guía paso a paso sobre cómo seleccionar los parámetros para construir tu modelo ARIMA y optimizarlo:
2. Guía paso a paso sobre cómo crear el modelo ARIMA de manera automática:




0 Comments