Las series temporales pueden ser estacionales (seasonal). Esto significa que los datos tienen un ciclo que se repite de manera regular, por ejemplo semanalmente, mensualmente o anualmente.
Algo que es importante es que la presencia de ciclos no significa que sea estacional. Para que un ciclo sea estacional éste tiene que repetirse de manera consistente a la misma frecuencia, sino es simplemente un ciclo no una estación.
Componentes de series temporales
Las series temporales pueden descomponerse en distintos componentes:
- Elemento de Moda (trend): Es la dirección que toman los datos a largo plazo
- Elemento estacional (seasonal): Variaciones sistemáticas relacionadas con las fechas, repetidas consistentemente a la misma frecuencia
- Elemento cíclico (cyclical): Periódico pero no estacional
- Elemento residual (residual): No sistemática, fluctuaciones de duración corta, ruido
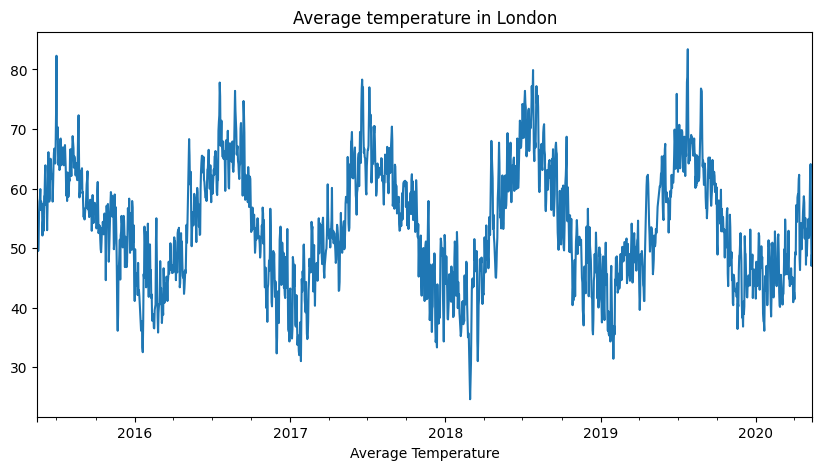
Ejemplo de datos temporales estacionales: Temperatura media en Londres desde 2016
Modelos de decomposición
Las series temporales pueden incluir cualquiera de esos componentes, sin embargo no todas los incluyen de la misma manera. Vamos a ver cómo usan estos elementos los modelos más comunes. Por simplicidad vamos a ignorar el componente cíclico.
Modelo aditivo
Estos modelos asumen que la serie temporal es la suma de sus elementos:
$$ y(t)=Trend+Seasonality+Residual $$
Además consideran que las magnitudes de los elementos estacional y residual son independientes de la moda.
Modelo multiplicativo
Estos modelos asumen que la serie temporal es la multiplicación de sus elementos:
$$ y(t)=Trend×Seasonality×Residual $$
El modelo supone que la estacionalidad los residuos dependen de la moda, este modelo se puede transformar en aditivo aplicando transformaciones logarítmicas:
$$ log(y(t))=log(Trend)+log(Seasonality)+log(Residual) $$
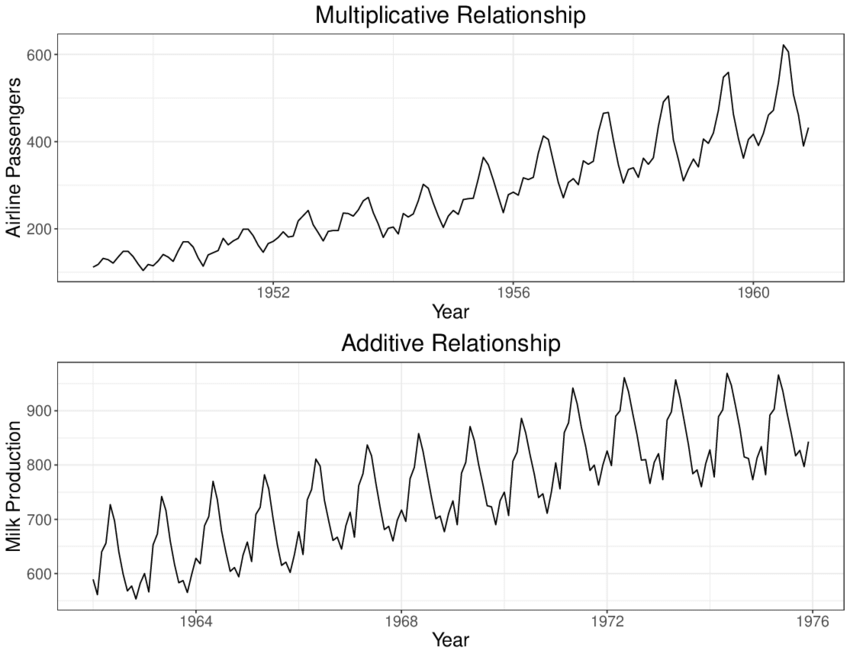
Modelos decomposición multiplicativo y aditivo
Otros modelos
Además de los dos modelos anteriores, hay otros modelos que se usan para decomponer series temporales:
- Pseudo-additive model (Modelo pseudo aditivo)
- Exponential smoothing (Suavización exponencial)
- Locally Estimated Scatterplot Smoothing (LOESS) (Suavizado de diagrama de dispersión estimado localmente)
- Frequency-based methods (métodos basados en frecuencia)
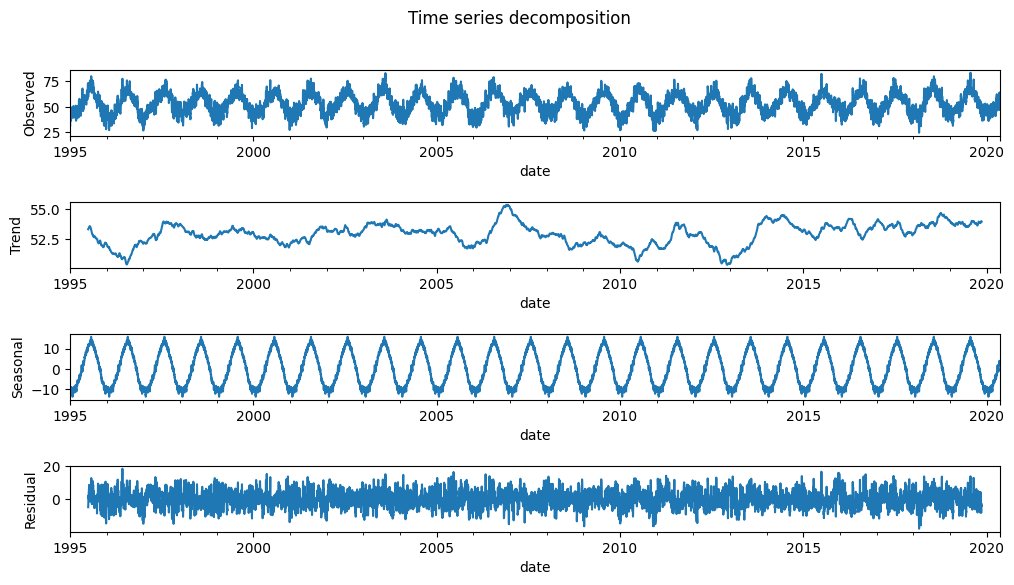
Serie temporal con decomposición aditiva de la temperatura de Londres desde 1995since 1995
Modelo SARIMA
En artículos anteriores introdujimos el modelo ARIMA. Este modelo es muy útil cuando no hay variaciones estacionales. Pueden modelar la moda de la serie temporal.
Sin embargo, si nuestros datos tiene estacionalidad necesitaremos un ARIMA Estacional o SARIMA (Seasonal ARIMA). El modelo ARIMA es una extensión del modelo ARIMA para poder modelar la componente estacional en datos de un solo atributo.
Un modelo SARIMA(p,d,q)(P,D,Q)m se define por siete parámetros. Tres vienen de la parte de ARIMA y otros cuatro caracterizan el modelado de la parte estacional:
Trend (moda)
- p : Orden autoregresivo de la moda
- d : Orden de la diferencia de la moda
- q : Orden de la media móvil de la moda
Seasonality (estacionalidad)
- P : Orden autoregresivo de la estacionalidad
- D : Orden de la diferencia de la estacionalidad
- Q : Orden de la media móvil de la estacionalidad
- m : Número de pasos temporales de un periodo estacional
Selección de parámetros
El primer parámetro que hay que definir es m. Este parámetro se define inspeccionando los datos iniciales y sabiendo qué representa.
Tras saber el número de pasos de un periodo estacional, los datos estarán decompuestos.
p y q se definirán como vimos en un artículo anterior inspeccionando el elemento de moda usando las gráficas ACF y PACF. d se definirá de tal manera que haga la moda estacionaria.
De igual manera, las gráficas ACF y PACF se usan para estimar los valores P y Q, mirando la correlación entre estaciones retrasadas. D se elegirá para que haga el periodo del elemento estacional estacionario.
También está la posibilidad de usar el auto-ARIMA una vez sabes la frecuencia de m para definir los otros seis parámetros.
Limitaciones
La limitación de los modelos SARIMA es que sólo pueden usarse cuando hay una estacionalidad única, por ejemplo podría darse el caso en el que haya estacionalidad durante el día, semana y año. Hay otros modelos para trabajar con ese tipo de datos como el TBABS.
Pruébalo
Decompón tus datos
Si quieres decomponer algunas series temporales puedes seguir la guía paso a paso de este Kaggle notebook:
Crea tu propio modelo auto-ARIMA
Aquí tienes una guía sobre cómo crear tu propio modelo ARIMA óptimo:




0 Comments