Una serie temporal (time series) es un conjunto de muestras ordenadas en el tiempo. El tiempo suele ser la variable independiente y el objetivo suele ser hacer una predicción futura.
Esto tiene muchas aplicaciones, como por ejemplo predecir las ventas, precios de acciones, temperaturas e incluso el número de casos COVID
Tradicionalmente, en las series temporales se han empleado métodos como ARIMA, Holt o ETS. Sin embargo en los últimos años han ganado importancia métodos de Machine Learning y Deep Learning.
ARIMA
ARIMA es uno de los métodos estadísticos tradicionales más populares, viene del inglés Auto-Regressive Integrated Moving Average (Media móvil integrada autorregresiva).
Se compone de 3 partes:
- AR: Auto regresiva (Auto-Regressive)
- I: Integrada (Integrated)
- MA: Media móvil (Moving Average)
Por ahora, vamos a suponer que la serie temporal no tiene un componente estacional.
Auto regresiva (AR)
Los modelos AR usan una combinación lineal de valores pasados de las variables de interés.
Se describen por el parámetro p, que se refiere al número de valores anteriores a tener en cuenta para la predicción.
La ecuación que corresponde a este modelo es:
$$y_t = c + \phi_1 y_{t-1} + \phi_2 y_{t-2} + …+ \phi_p y_{t-p} + \varepsilon_t$$
- c : Representa una constate o drift
- y : Representa al valor actual de la variable de interés(t), valor de un paso temporal anterior (t-1), valor de dos pasos temporales anteriores (t-2)…
- ϕ : Son los coeficientes que se necesitan calcular ajustándose a los datos de entrada
- p : Es el número de coeficientes que queremos que tenga nuestro modelo
- εₜ : Es el término de error, que es ruido blanco
Media móvil (MA)
Los modelos MA usan una combinación lineal de valores de erro pasados en lugar de previos valores de la variable de interés.
Se describen por el parámetro q, que representa el número de valores erróneos anteriores a considerar para la predicción.
La ecuación que corresponde a este modelo es:
$y_t = c + \theta_1 \varepsilon_{t-1} + \theta_2 \varepsilon_{t-2} + … + \theta_q \varepsilon_{t-q} + \varepsilon_t$
- c : Representa una constate o drift
- y : Representa la variable de interés
- θ : Son los coeficientes que se necesitan calcular ajustándose a los datos de entrada
- q : Es el número de coeficientes que queremos que tenga nuestro modelo
- εₜ : Es el término de error, que es ruido blanco
Integrada (I)
Se refiere a la diferenciación de los datos de la serie temporal. Esto no representa un modelo en sí mismo, es una manera de expandir la aplicabilidad de los modelos AR, MA o ARMA. Los modelos ARMA (sin la I) sólo son válidos para series temporales estacionarias.
¿Qué significa estacionario?
En términos simples, una serie temporal es estacionaria se su media y varianza no varían con el tiempo.
Esto se puede conseguir de varias maneras:
- Diferenciación de la serie temporal
- Transformación de cuadrados (power transformation)
- Transformación logarítmica
Diferenciación de series temporales
Diferenciación se refiere a calcular la diferencia entre el periodo actual y el periodo anterior. En algunos campos, como en finanzas, se mira el cambio percentual, que simplemente se basa en aplicar un factor de 100 a la transformación anterior.
¿Cómo hacemos un modelo ARIMA estacionario?
Le podemos aplicar la diferenciación a yₜ, que está en la parte izquierda de la ecuación y dejamos la parte de la derecha sin tocar. Aplicaremos diferenciación tantas veces como sea necesario hasta obtener una serie temporal estacionaria. Esto se especifica a través del parámetro d:
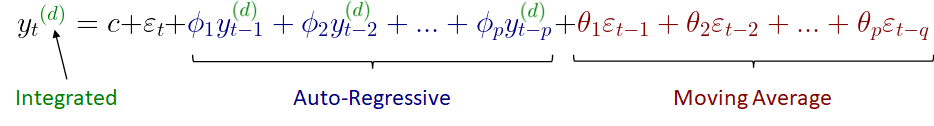
Tras eso tendremos tres modelos ARIMA más la constante c y el error εₜ que es ruido blanco.
La constante se calculará durante el entrenamiento del modelo, sin embargo, el error será la diferencia entre nuestra predicción y el valor correcto, y sólo lo podremos calcular una vez sepamos el valor correcto de nuestra variable de interés yₜ.
¿Cómo elegimos los parámetros p, q y d?
En un artículo futuro de series temporales os enseñaremos cómo seleccionar esos parámetros.



0 Comments