Part II: Precision/Recall and Sensitivity/Specificity

In the previous article on evaluation metrics for classification problems we explained that accuracy is a very useful metric and very easy to interpret. However, if the dataset we have is not balanced, it will be completely useless.

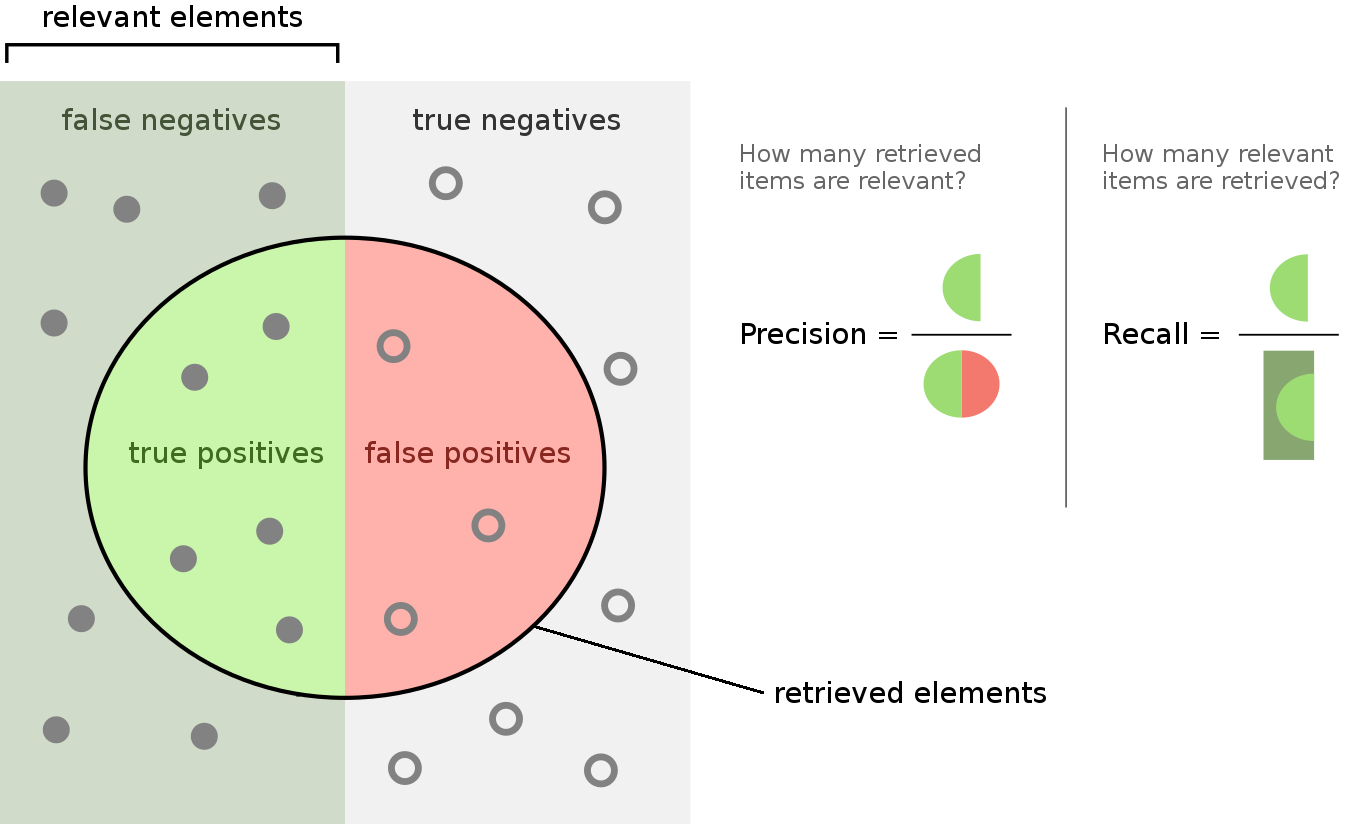
We also defined what a confusion matrix is, in which we defined four categories among our predictions: True Positives, True Negatives, False Positives and False Negatives. We can use this information to evaluate our model despite having imbalanced data.

Precision-Recall

On the one hand, precision indicates the proportion of the relevant or positive samples predicted by our model that are actually positive.

$$ \text{Precision} = \frac{TP}{TP + FP} $$

On the other hand, recall indicates the proportion of relevant or positive samples predicted by the model with respect to all the actual positive samples.

$$ \text{Recall} = \frac{TP}{TP + FN} $$

The following picture illustrates both metrics:

As mentioned before, these metrics are robust against imbalanced data. A way of taking both into account to evaluate the model is considering the Fbeta-score:

$$ F_{ \beta}\text{ -}score = \frac{(1 + \beta^2) \times Precision \times Recall}{\beta^2 \times Precision + Recall} $$

The Fbeta-score is defined as the harmonic mean of the precision and recall. The beta parameter can be tuned depending on the situation:

• If the objective of the analyst is to reduce the FP results, then a small beta should be chosen to increase the importance of the precision in the metric
• If the emphasis is made on reducing the FN, then a large beta must be selected to increase the relevance of the recall in the metric
• For achieving a balanced performance on both FP and FN, then beta equal to 1 will be the obvious value for beta. In this scenario, this metric receives the name of F1-score (being the most common case) and the previous equation can be rewritten as:

$$ F_1\text{-}score = 2 \times \frac{Precision \times Recall}{Precision + Recall} $$

Sensitivity-Specificity

Another way of evaluating a model is by means of sensitivity and specificity. These metrics are also robust against imbalanced datasets.

Sensitivity indicates how well the positive class was predicted and it is equivalent to the recall:

$$ \text{Sensitivity} = \frac{TP}{TP + FN} $$

Specificity is the complement metric and it indicates how well the negative class was predicted:

$$ \text{Specificity} = \frac{TN}{FP + TN} $$

In the same way as with precision and recall, both metrics can be combined, this time with the so-called geometric mean or G-Mean:

$$ \text{G-Mean} = \sqrt{Sensitivity \times Specificity} $$